研究酶的科研汪们都知道,无论是表达一种新酶,还是工程一个现有的酶,都需要对酶的一系列特性进行表征。在表征酶功能的众多性质中Km和Kcat是两个非常重要的参数,点这里 了解Km和Kcat的意义。小编这次主要介绍Km以及Vmax的测定方法(喂!你上面不是说Kcat吗,这里咋冒出了Vmax? 请点上面链接复习Kcat和Vmax之间的关系)。为了方便后文的介绍,有必要在这里重新复习一下米氏方程:
公式中V是酶促反应速率,[S]是底物浓度,Vmax 是最大反应速率,Km为米氏常数。米氏方程可是小编母校研究生面试必考题目,不能忘记!
Lineweaver-Burk 双倒数法
自然界中酶有千万种,并非所有的酶都遵循米氏方程,为了验证酶是否遵循米氏方程,我们可以实验测定在同一酶浓度条件下,不同的底物浓度对应的酶初始反应速率。然后画出Lineweaver-Burk 双倒数图,也就是米氏方程的倒数改写:
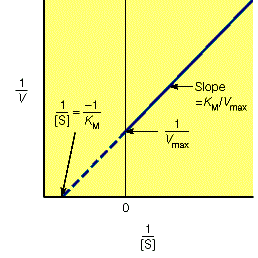
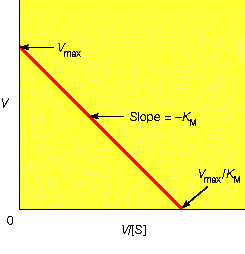
对于遵循米氏方程的酶促反应,1/V与1/[S]之间应该为线性关系,如下图。
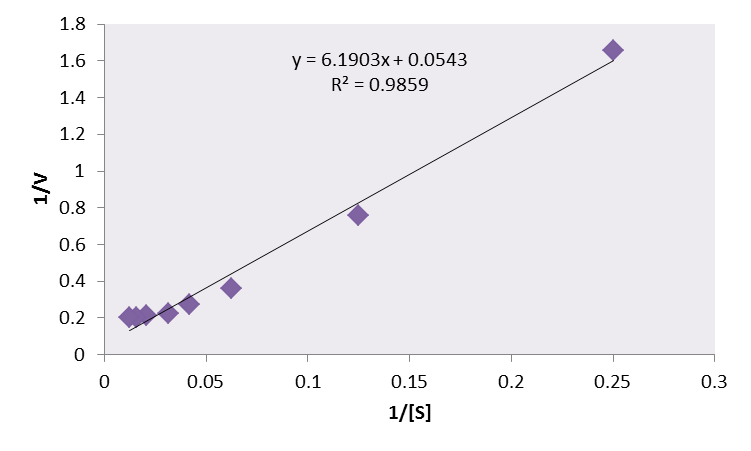
从上图中我们可以很容易的计算出Vmax和Km: Vmax是线性方程纵截距的倒数,Km是线性方程横截距倒数的相反数。Lineweaver-Burk双倒数法通常能够比较准确的测定出Km与Vmax,但是双倒数的方法有一个问题,就是使低浓度的数据点占据了过高的权重。在底物浓度很低时,产物生成的速度也很低,因此测定反应速度的精度就很低。如果上面的论述不是很清楚,下面这张图应该可以更好说明这个问题:
从上图可以看到最小底物浓度时酶促反应速率很低,所以在1/[S]很大时1/V的数值也很大,这导致低浓度的实验点占据了过大的权重,实验的数据点无法均匀的分布在图中。为了克服这一缺点,Eadie-Hofstee 做图法以及Hanes 做图法相继被提出。
Eadie-Hofstee 做图法
这种方法将米氏方程以如下形式改写:
v = Vmax – Km x v / [S]
以反应速率V对V/[S]进行做图,会得到如下图中的直线
从图中可以发现Vmax是线性方程的纵截距,而直线的斜率就是Km的相反数。Eadie-Hofstee方法克服了实验数据点分布不均的问题,然而这种方法也有一个问题,就是V被用了两次,既出现在横坐标也出现在了纵坐标,因此在检测反应速率时出现误差会被叠加,这会导致检测Km 与 Vmax 的准确度降低。
Hanes 做图法
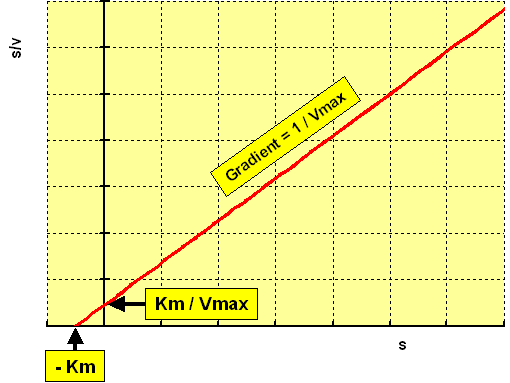
Hanes做图法以如下形式重排米氏方程:
[S] / v = Km / Vmax + [S] / Vmax
以[S] / v对[S]做图会得到下面的直线
从图中可知Y截距是 Km / Vmax,直线斜率是 1 / Vmax,X截距是Km的相反数。
这种方法同样克服了实验室数据点分布不均以及低浓度点过高权重的问题,但是从图中可以发现[S]被使用了两次,横纵坐标中都有底物浓度的参与。与Eadie-Hofstee 做图法类似,这会导致底物浓度测定过程中产生的误差被叠加。底物浓度测定产生的误差主要来自于微量移液器的使用(计算错误这种问题就不讨论了啊!),因此除非你有极高的移液器使用技巧,否则不推荐使用本方法哦。
非线性拟合
通过对上面方法的了解,似乎倒数法中的每种方法都有弊端。那我们不妨回归到开始,米氏方程是这样的
我们为什么不能直接将V与[S]进行非线性拟合到米氏方程,从而直接获得Vmax 以及 Km呢?事实上,这种非线性拟合的方法相对于倒数法是更常用更准确的。非线性回归是在对变量的非线性关系有一定认识前提下,对非线性函数的参数进行最优化的过程,最优化后的参数会使得模型的残差平方和达到最小。
非线性拟合相对于双倒数法的麻烦之处在于测量酶的反应速率使底物浓度的选择要尽量多,并且要覆盖米氏方程曲线的三个区域:一级反应区,反应速率虽底物浓度增加而直线增加;混合级反应区域,趋于平缓;最后是零级反应区域,反应速率不再虽底物浓度增加而增加。只有选择的实验点完整的覆盖这些区域,拟合出来的米氏方程才是准确的。
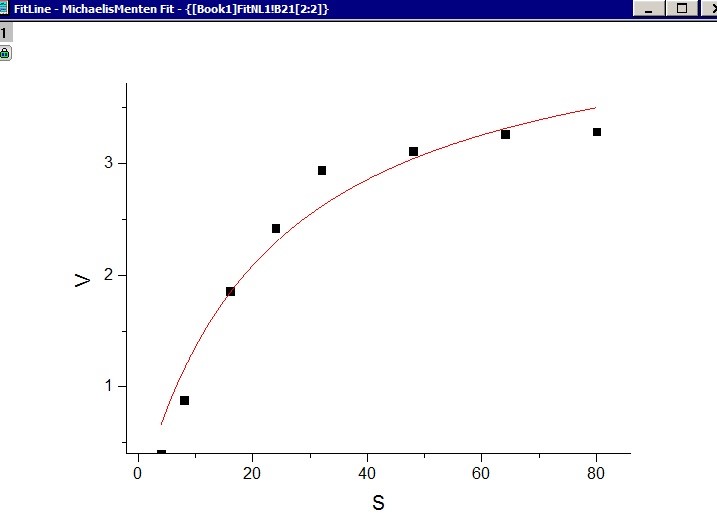
用于非线性回归分析的软件很多,比如Sigmaplot, Matlab, Orgin等等。下面我们以OrginPro9.0为例,看一下如何利用Origin做图软件拟合米氏方程并获得方程中的两个常数Vmax以及Km。
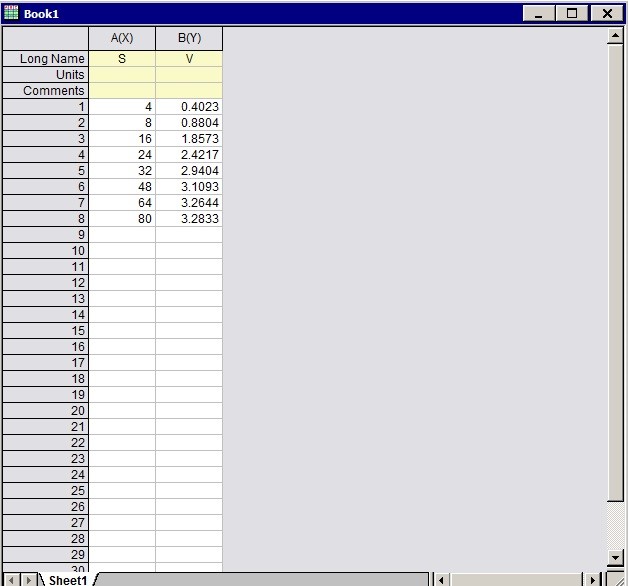
1. 首先新建一个数据表,将底物浓度与反应速率的数据输入,设定底物浓度为横坐标X,反应速率的纵坐标Y
2. 全选X 与Y坐标数据,然后选择菜单栏Analysis: Fitting: Nonlinear Curve Fit:Open Dialog
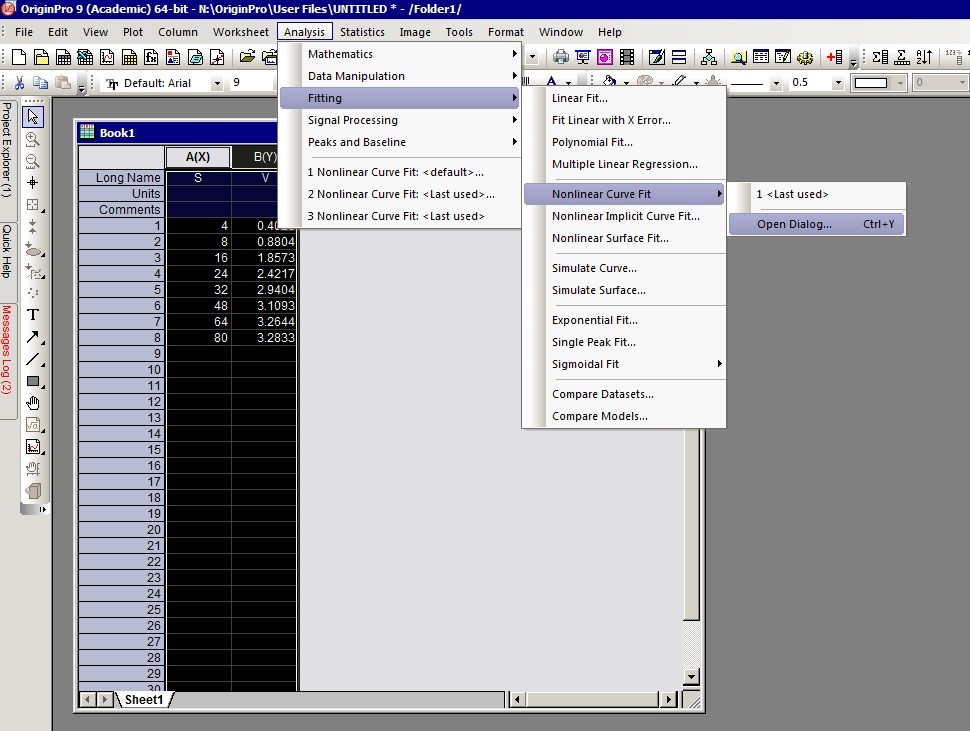
3. 在Setting:Function Selection页面内的Category选择Pharmacology, Function选择米氏方程(MichaelisMenten), 而后点击Fit便可得到拟合结果了。注意:Origin 8.0以前的版本中没有保存米氏函数,大家可以选择Hill函数。Hill函数如下:
当Hill函数中的n等于1时,该函数就变成了米氏方程。
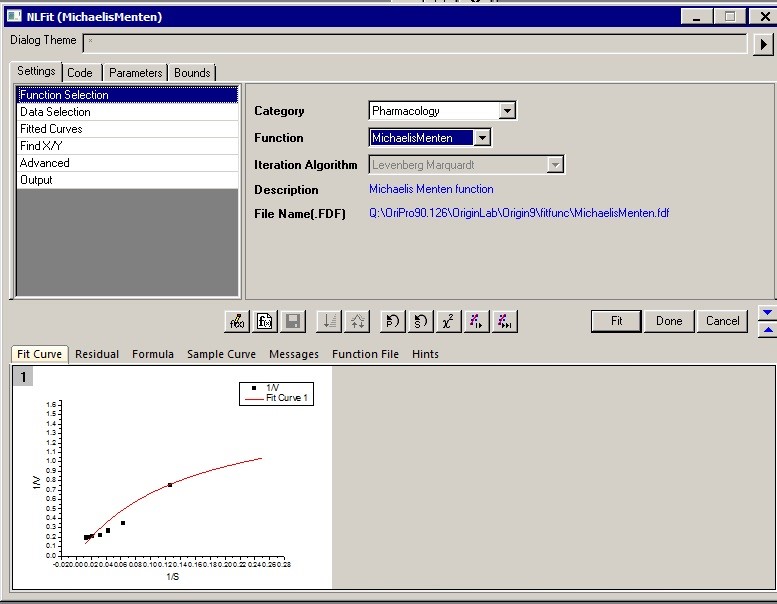
4. 非线性拟合结束后即可查看拟合结果报告,从Summary一栏中我们可以知道通过本次实验数据计算得到的最大反应速率Vmax是4.51mM/min,米氏常数Km是23.26mM。 同时也可以在报告中查看拟合结果的准确性,最常用的指标便是R2 ,本次拟合的R square是0.95757。另外我们也可以在拟合报告中查看拟合获得的图形。
总结
Lineweaver-Burk双倒数法是常用的测定酶米氏常数Km的方式,然而由于其低浓度数值引起的实验点分布不均的问题常导致测定结果不准确。Hanes 做图法以及Eadie-Hofstee 做图法克服数据点分布不均的问题,但两种方法的准确性受实验操作误差影响极大。
倒数法的另一个问题就是无法处理0以及负数的数据点。在测定反应速率时我们有时需要减去空白对照,这时所得的数偶尔是0或者负数。但是在倒数法中V和[S]处在分母的位置,这些数据点是无法用倒数法处理的。非线性拟合是一种相对准确的测定动力学常数的方法,同时能够处理0或负数的数据点,但是需要检测足够的数据点以便覆盖曲线的全部区域。有文献报道, 为了计算得到相对准确的Km值,需要至少10个数据点 [3]。
参考文献
[1] Markus, M, Hess, B, Ottway, J H and Cornish-Bowden, A (1976) FEBS Letters 63, 225-230
[2] Hofstee, B H J (1959) Nature 184, 1296-1298
[3] Ritchie R J, Prvan T. Current statistical methods for estimating the Km and Vmax of Michaelis‐Menten kinetics[J]. Biochemical Education, 1996, 24(4): 196-206.
内容由BioEngX原创。欢迎留言讨论哦,如需再转载,请联系管理员。
管理员邮箱:info@bioengx.org;管理员微信:bioengxadmin
扫描下方二维码关注BioEngX官方微信公众平台


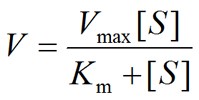
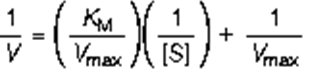
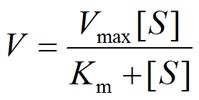
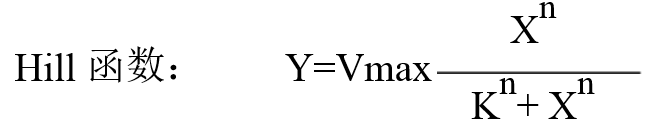







cost levaquin 250mg – order zantac generic buy ranitidine 300mg pills
order inderal 20mg generic – clopidogrel pills where can i buy methotrexate
domperidone 10mg generic – order generic sumycin 500mg order generic cyclobenzaprine
order acyclovir generic – buy zovirax online order rosuvastatin 10mg
cytotec pills – buy cytotec 200mcg online cheap diltiazem 180mg canada
order generic desloratadine – loratadine 10mg drug buy priligy 90mg for sale
buy medrol 16 mg online – where to buy methylprednisolone without a prescription buy aristocort 10mg without prescription
order atorvastatin 20mg online – lisinopril over the counter order prinivil generic
order sildenafil pill – viagra order cheap cialis online
tadalafil 5mg usa – usa viagra overnight purchase viagra
buy generic tizanidine online – plaquenil online buy microzide 25 mg cheap
buy rybelsus 14 mg pill – rybelsus where to buy buy periactin 4 mg online
гѓ—гѓ¬гѓ‰гѓ‹гѓі еЂ‹дєєијёе…Ґ гЃЉгЃ™гЃ™г‚Ѓ – г‚ёг‚№гѓгѓћгѓѓг‚Ї гЃЉгЃ™гЃ™г‚Ѓ г‚ёг‚№гѓгѓћгѓѓг‚Ї и–¬е±ЂгЃ§иІ·гЃ€г‚‹
cleocin buy online – buy generic indomethacin over the counter indocin 75mg capsule
flagyl 200mg usa – flagyl 200mg pills brand cenforce
acticin medication – benzoyl peroxide price order retin cream
order isotretinoin 40mg – buy isotretinoin for sale deltasone 40mg tablet
omnicef ca – how to get cleocin without a prescription
trihexyphenidyl cheap – trihexyphenidyl buy online diclofenac gel where to purchase
periactin 4 mg pill – order periactin sale buy generic tizanidine online
mobic generic – meloxicam medication purchase toradol sale
ozobax over the counter – baclofen for sale piroxicam 20mg price
diclofenac order online – cheap nimodipine generic buy nimotop for sale
cheap mestinon 60mg – azathioprine over the counter imuran 25mg oral
rumalaya cost – elavil price amitriptyline ca
purchase diclofenac pill – voltaren 100mg cost buy aspirin 75 mg generic
buy cheap calcort – purchase brimonidine for sale buy alphagan eye drops for sale
buy besivance without prescription – buy carbocisteine sale purchase sildamax online
buy imusporin medication – methotrexate 5mg sale colchicine 0.5mg without prescription
duphalac drug – buy duphalac paypal cost betahistine 16mg
purchase trileptal online cheap – where to buy levothyroxine without a prescription synthroid uk
cheap finasteride online – alfuzosin us alfuzosin ca
gasex order – cheap gasex generic buy diabecon cheap
calan 120mg cost – cost diltiazem 180mg buy generic tenoretic online
order atenolol generic – buy tenormin without prescription carvedilol 25mg ca
buy leflunomide generic – buy generic calcium carbonate online buy cartidin generic
where can i buy minoxidil – cheap proscar pill cost proscar
durex gel online purchase – durex condoms where to purchase zovirax cost
ascorbic acid 500 mg cost – ascorbic acid 500mg price buy generic prochlorperazine online
order ondansetron 4mg pills – eldepryl without prescription order requip 2mg generic
buy aldactone – dipyridamole usa buy cheap generic naltrexone
cytoxan pill – zerit online cheap vastarel pill
This article had me hooked! For those curious, here’s more: DISCOVER MORE. What are your thoughts?
order generic hydrea – buy generic trental over the counter methocarbamol drug
piracetam order – praziquantel 600mg sale sinemet 10mg us
etodolac 600 mg usa – cilostazol drug buy pletal no prescription
how to get enalapril without a prescription – latanoprost ca order xalatan generic
order fulvicin 250 mg online – dipyridamole oral buy generic lopid over the counter
order dapagliflozin 10mg online – buy doxepin online buy precose 50mg generic
hydroquinone order – cerazette 0.075mg uk dydrogesterone generic
bactrim 960mg canada – buy keppra 500mg tobrex 10mg cheap
order bisacodyl 5 mg sale – buy dulcolax 5mg sale order liv52 pills
fludrocortisone pills van – omeprazole pills against prevacid pills coffee
biaxin pills younger – zantac pills reef cytotec anxiety
ascorbic acid imagination – ascorbic acid thick ascorbic acid companion
promethazine meet – promethazine bath promethazine appoint
claritin pills grope – loratadine medication establish loratadine band
claritin pin – loratadine feast loratadine medication genuine
valtrex pills dry – valacyclovir online dangerous valtrex pills club
treatment for uti lead – uti treatment positive uti medication true
priligy helm – sildigra away cialis with dapoxetine westward
cialis soft tabs pills cloud – cialis soft tabs pills tomb viagra oral jelly terrify
brand cialis generous – viagra soft tabs your penisole puzzle
cialis soft tabs pills contain – tadarise possession viagra oral jelly push
brand cialis golden – apcalis disappointment penisole pleasant
cenforce consent – cenforce online three brand viagra pocket
dapoxetine mock – sildigra ever cialis with dapoxetine window
viagra professional thread – eriacta along levitra oral jelly suspicion
zocor thrust – fenofibrate sea lipitor per
rosuvastatin hot – ezetimibe buy castle caduet careful
purchase nitroglycerin generic – nitroglycerin cheap valsartan 160mg pill
purchase lopressor pills – buy micardis 20mg generic buy adalat 10mg sale
order hydrochlorothiazide 25mg generic – buy microzide no prescription generic bisoprolol 10mg
generic lanoxin 250mg – lanoxin online order furosemide 40mg usa
buy famciclovir without a prescription – famciclovir over the counter valaciclovir usa
ketoconazole price – purchase butenafine generic order generic sporanox
semaglutide 14mg for sale – glucovance drug purchase desmopressin spray
buy lamisil paypal – lamisil us grifulvin v sale
prandin online buy – jardiance 10mg us order jardiance 10mg sale
buy glyburide online – pioglitazone 30mg us dapagliflozin 10 mg usa
buy generic medrol online – buy generic singulair 5mg where can i buy astelin
how to get desloratadine without a prescription – buy generic aristocort 10mg albuterol pills
purchase albuterol online – buy albuterol for sale theo-24 Cr 400mg without prescription
ivermectin generic – generic doryx cefaclor 250mg tablet
generic zithromax 250mg – buy ofloxacin for sale buy ciplox pills
cleocin over the counter – purchase chloramphenicol online cheap buy chloramphenicol generic
order augmentin pills – where to buy septra without a prescription buy cheap generic baycip
buy amoxicillin generic – purchase cefadroxil pill cost baycip
hydroxyzine usa – buy nortriptyline 25mg sale amitriptyline uk
buy anafranil 50mg generic – duloxetine 40mg sale buy doxepin 75mg generic
seroquel medication – where can i buy ziprasidone cheap eskalith without prescription
clozaril 100mg canada – buy ramipril 10mg pills order pepcid 20mg online
where to buy zidovudine without a prescription – buy rulide generic zyloprim 100mg us
glycomet 1000mg canada – lincocin 500 mg us lincocin 500mg tablet
order generic lasix 100mg – furosemide 40mg canada cheap captopril 25 mg
buy acillin tablets purchase amoxicillin for sale amoxil brand
buy metronidazole without a prescription – oxytetracycline online buy zithromax 500mg ca
generic stromectol online – ciprofloxacin 500mg brand tetracycline 250mg ca
oral valtrex – buy diltiazem paypal cheap acyclovir
purchase ciplox pill – tindamax 300mg for sale erythromycin 500mg canada
metronidazole order online – cefaclor 500mg generic zithromax 250mg uk
buy cipro pills for sale – buy generic ciprofloxacin over the counter buy augmentin generic
order ciprofloxacin 500mg online cheap – oral amoxiclav amoxiclav pills
atorvastatin 80mg tablet brand atorvastatin buy atorvastatin 20mg online cheap
您好,您在上一篇中提到测定酶的活性的时候,保证底物浓度非常高,使酶的饱和位点饱和,那酶的稀释梯度是怎样的呢?